Clustering with Noise Point Detection

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import genieclust

Let’s load an example dataset that can be found at the hdbscan [14] package’s project site:

dataset = "hdbscan"
X = np.loadtxt("%s.data.gz" % dataset, ndmin=2)
labels_true = np.loadtxt("%s.labels0.gz" % dataset, dtype=np.intp) - 1
n_clusters = len(np.unique(labels_true[labels_true>=0]))

Here are the “reference” labels as identified by an expert (of course, each dataset might reveal many different clusterings that users might find useful for whatever their goal is). The label -1 designates noise points (light grey markers).

genieclust.plots.plot_scatter(X, labels=labels_true, alpha=0.5)
plt.title("(n=%d, true n_clusters=%d)" % (X.shape[0], n_clusters))
plt.axis("equal")
plt.show()

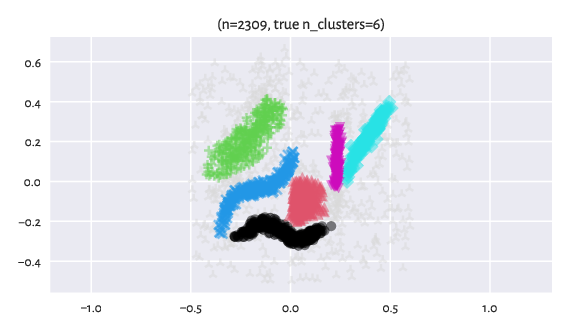
Figure 10 Reference labels

Smoothing Factor

The genieclust package allows for clustering with respect to a mutual reachability distance, \(d_M\), known from the HDBSCAN* algorithm [2]. It is parameterised by a smoothing factor, \(M\ge 2\), which controls how eagerly we tend to classify points as noise.

Instead of the ordinary (usually Euclidean) distance between two points \(i\) and \(j\), \(d(i,j)\), we take \(d_M(i,j)=\max\{ c_M(i), c_M(j), d(i, j) \}\), where the \(M\)-core distance \(c_M(i)\) is the distance between \(i\) and its \((M-1)\)-th nearest neighbour.

Here are the effects of playing with the \(M\) parameter (we keep the default gini_threshold):

Ms = [2, 5, 10, 25]
for i in range(len(Ms)):
    g = genieclust.Genie(n_clusters=n_clusters, M=Ms[i])
    labels_genie = g.fit_predict(X)
    plt.subplot(2, 2, i+1)
    genieclust.plots.plot_scatter(X, labels=labels_genie, alpha=0.5)
    plt.title("(gini_threshold=%g, M=%d)"%(g.gini_threshold, g.M))
    plt.axis("equal")
plt.show()

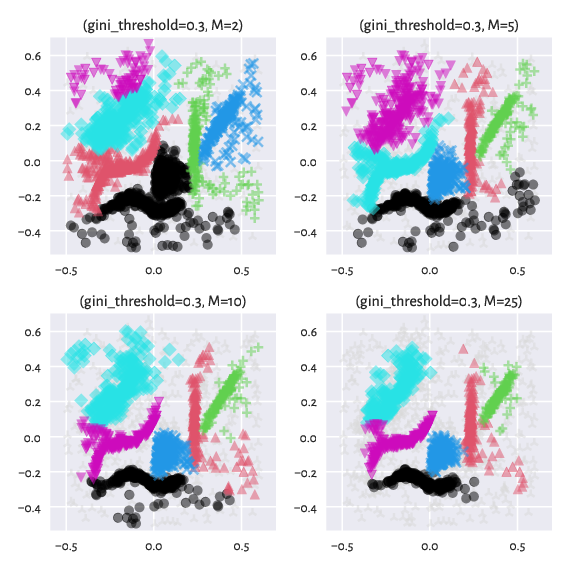
Figure 11 Labels predicted by Genie with noise point detection

We can also first identify the noise points with Genie, remove them temporarily from the dataset, and then apply the clustering procedure once again but now with respect to the original distance (here: Euclidean):

# Step 1: Noise point identification
g1 = genieclust.Genie(n_clusters=n_clusters, M=50)
labels_noise = g1.fit_predict(X)
non_noise = (labels_noise >= 0) # True == non-noise point
# Step 2: Clustering of non-noise points:
g2 = genieclust.Genie(n_clusters=n_clusters)
labels_genie = g2.fit_predict(X[non_noise, :])
# Replace old labels with the new ones:
labels_noise[non_noise] = labels_genie
# Scatter plot:
genieclust.plots.plot_scatter(X, labels=labels_noise, alpha=0.5)
plt.title("(gini_threshold=%g, noise points removed first; M=%d)"%(g2.gini_threshold, g1.M))
plt.axis("equal")
plt.show()

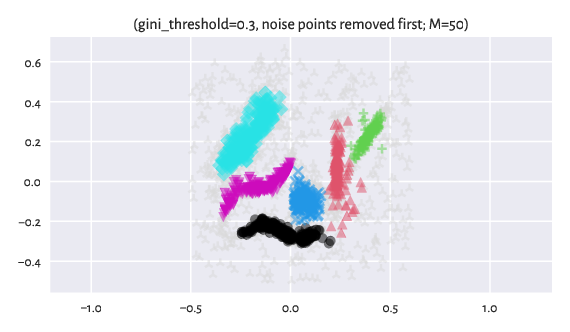
Figure 12 Labels predicted by Genie when noise points were removed from the dataset

Contrary to the excellent implementation of HDBSCAN* that is featured in the hdbscan package [14] and which also relies on a minimum spanning tree with respect to \(d_M\), in our case, we still have the hierarchical Genie [9] algorithm under the hood. It means that we can request a specific number of clusters. Moreover, we can easily switch between partitions of finer or coarser granularity: they are appropriately nested.

ncs = [4, 5, 6, 7, 8, 9]
for i in range(len(ncs)):
    g = genieclust.Genie(n_clusters=ncs[i])
    labels_genie = g.fit_predict(X[non_noise, :])
    plt.subplot(3, 2, i+1)
    labels_noise[non_noise] = labels_genie
    genieclust.plots.plot_scatter(X, labels=labels_noise, alpha=0.5)
    plt.title("(n_clusters=%d)"%(g.n_clusters))
    plt.axis("equal")
plt.show()

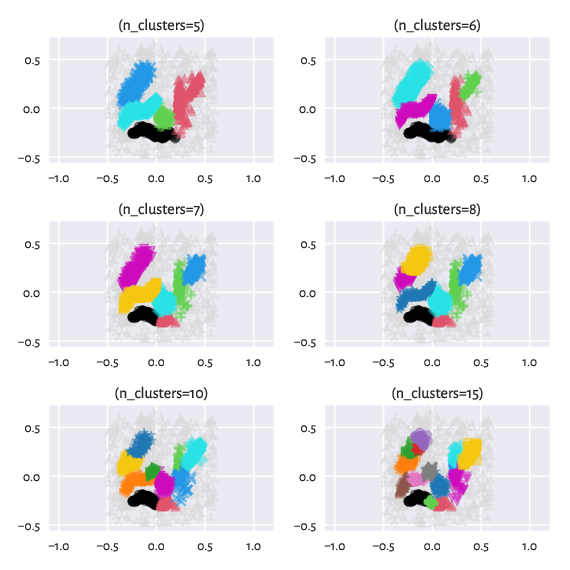
Figure 13 Labels predicted by Genie when noise points were removed from the dataset – different number of clusters requested

A Comparision with HDBSCAN*

Here are the results returned by hdbscan with default parameters:

import hdbscan
h = hdbscan.HDBSCAN()
labels_hdbscan = h.fit_predict(X)
genieclust.plots.plot_scatter(X, labels=labels_hdbscan, alpha=0.5)
plt.title("(min_cluster_size=%d, min_samples=%d)" % (
    h.min_cluster_size, h.min_samples or h.min_cluster_size))
plt.axis("equal")
plt.show()

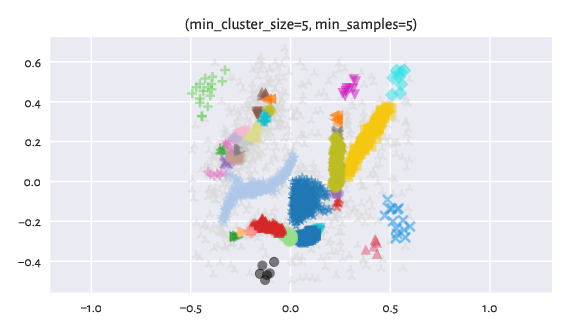
Figure 14 Labels predicted by HDBSCAN*.

By tuning up min_cluster_size and/or min_samples (which corresponds to our M-1; by the way, min_samples defaults to min_cluster_size if not provided explicitly), we can obtain a partition that is even closer to the reference one:

mcss = [5, 10, 25]
mss = [5, 10]
for i in range(len(mcss)):
    for j in range(len(mss)):
        h = hdbscan.HDBSCAN(min_cluster_size=mcss[i], min_samples=mss[j])
        labels_hdbscan = h.fit_predict(X)
        plt.subplot(3, 2, i*len(mss)+j+1)
        genieclust.plots.plot_scatter(X, labels=labels_hdbscan, alpha=0.5)
        plt.title("(min_cluster_size=%d, min_samples=%d)" % (
            h.min_cluster_size, h.min_samples or h.min_cluster_size))
        plt.axis("equal")
plt.show()

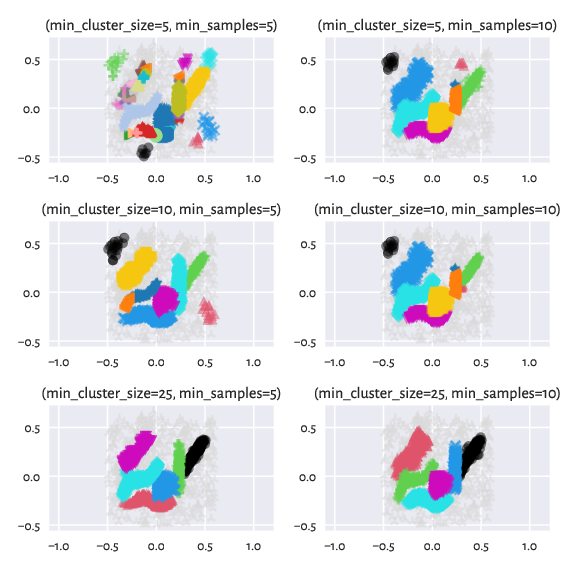
Figure 15 Labels predicted by HDBSCAN* – different settings

Neat.