gclust: Hierarchical Clustering Algorithm Genie¶
Description¶
A reimplementation of Genie - a robust and outlier resistant clustering algorithm by Gagolewski, Bartoszuk, and Cena (2016). The Genie algorithm is based on the minimum spanning tree (MST) of the pairwise distance graph of a given point set. Just like the single linkage, it consumes the edges of the MST in an increasing order of weights. However, it prevents the formation of clusters of highly imbalanced sizes; once the Gini index (see gini_index()) of the cluster size distribution raises above gini_threshold, the merging of a point group of the smallest size is enforced.
The clustering can also be computed with respect to the mutual reachability distances (based, e.g., on the Euclidean metric), which is used in the definition of the HDBSCAN* algorithm (see Campello et al., 2013). If \(M>1\), then the mutual reachability distance \(m(i,j)\) with a smoothing factor \(M\) is used instead of the chosen “raw” distance \(d(i,j)\). It holds \(m(i,j)=\max(d(i,j), c(i), c(j))\), where the core distance \(c(i)\) is the distance to the \(i\)-th point’s (\(M-1\))-th nearest neighbour. This makes “noise” and “boundary” points being more “pulled away” from each other.
The Genie correction together with the smoothing factor \(M>1\) (note that \(M=2\) corresponds to the original distance) gives a version of the HDBSCAN* algorithm that is able to detect a predefined number of clusters. Hence it does not dependent on the DBSCAN’s eps parameter or the HDBSCAN’s min_cluster_size one.
Usage¶
gclust(d, ...)
## Default S3 method:
gclust(
d,
gini_threshold = 0.3,
distance = c("euclidean", "l2", "manhattan", "cityblock", "l1", "cosine"),
verbose = FALSE,
...
)
## S3 method for class 'dist'
gclust(d, gini_threshold = 0.3, verbose = FALSE, ...)
## S3 method for class 'mst'
gclust(d, gini_threshold = 0.3, verbose = FALSE, ...)
genie(d, ...)
## Default S3 method:
genie(
d,
k,
gini_threshold = 0.3,
distance = c("euclidean", "l2", "manhattan", "cityblock", "l1", "cosine"),
M = 1L,
postprocess = c("boundary", "none", "all"),
detect_noise = M > 1L,
verbose = FALSE,
...
)
## S3 method for class 'dist'
genie(
d,
k,
gini_threshold = 0.3,
M = 1L,
postprocess = c("boundary", "none", "all"),
detect_noise = M > 1L,
verbose = FALSE,
...
)
## S3 method for class 'mst'
genie(
d,
k,
gini_threshold = 0.3,
postprocess = c("boundary", "none", "all"),
detect_noise = FALSE,
verbose = FALSE,
...
)
Arguments¶
|
a numeric matrix (or an object coercible to one, e.g., a data frame with numeric-like columns) or an object of class |
|
further arguments passed to |
|
threshold for the Genie correction, i.e., the Gini index of the cluster size distribution; threshold of 1.0 leads to the single linkage algorithm; low thresholds highly penalise the formation of small clusters |
|
metric used to compute the linkage, one of: |
|
logical; whether to print diagnostic messages and progress information |
|
the desired number of clusters to detect, \(k=1\) with \(M>1\) acts as a noise point detector |
|
smoothing factor; \(M \leq 2\) gives the selected |
|
one of |
|
whether the minimum spanning tree’s leaves should be marked as noise points, defaults to |
Details¶
As in the case of all the distance-based methods, the standardisation of the input features is definitely worth giving a try. Oftentimes, more sophisticated feature engineering (e.g., dimensionality reduction) will lead to more meaningful results.
If d is a numeric matrix or an object of class dist, mst() will be called to compute an MST, which generally takes at most \(O(n^2)\) time. However, by default, a faster algorithm based on K-d trees is selected automatically for low-dimensional Euclidean spaces; see mst_euclid from the quitefastmst package.
Once a minimum spanning tree is determined, the Genie algorithm runs in \(O(n \sqrt{n})\) time. If you want to test different gini_thresholds or ks, it is best to compute the MST first explicitly.
According to the algorithm’s original definition, the resulting partition tree (dendrogram) might violate the ultrametricity property (merges might occur at levels that are not increasing w.r.t. a between-cluster distance). gclust() automatically corrects departures from ultrametricity by applying height = rev(cummin(rev(height))).
Value¶
gclust() computes the entire clustering hierarchy; it returns a list of class hclust; see hclust. Use cutree to obtain an arbitrary k-partition.
genie() returns a k-partition - a vector whose i-th element denotes the i-th input point’s cluster label between 1 and k If detect_noise is TRUE, missing values (NA) denote noise points.
References¶
Gagolewski, M., Bartoszuk, M., Cena, A., Genie: A new, fast, and outlier-resistant hierarchical clustering algorithm, Information Sciences 363, 2016, 8-23, doi:10.1016/j.ins.2016.05.003
Campello, R.J.G.B., Moulavi, D., Sander, J., Density-based clustering based on hierarchical density estimates, Lecture Notes in Computer Science 7819, 2013, 160-172, doi:10.1007/978-3-642-37456-2_14
Gagolewski, M., Cena, A., Bartoszuk, M., Brzozowski, L., Clustering with minimum spanning trees: How good can it be?, Journal of Classification 42, 2025, 90-112, doi:10.1007/s00357-024-09483-1
See Also¶
The official online manual of genieclust at https://genieclust.gagolewski.com/
Gagolewski, M., genieclust: Fast and robust hierarchical clustering, SoftwareX 15:100722, 2021, doi:10.1016/j.softx.2021.100722
mst() for the minimum spanning tree routines
normalized_clustering_accuracy() (amongst others) for external cluster validity measures
Examples¶
library("datasets")
data("iris")
X <- jitter(as.matrix(iris[2:3]))
h <- gclust(X)
y_pred <- cutree(h, 3)
y_test <- as.integer(iris[,5])
plot(X, col=y_pred, pch=y_test, asp=1, las=1)
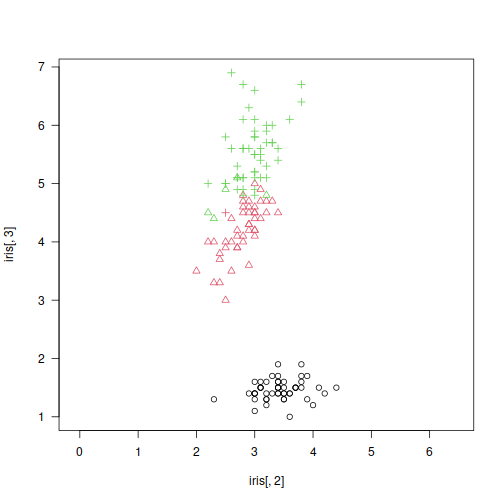
adjusted_rand_score(y_test, y_pred)
## [1] 0.6956362
normalized_clustering_accuracy(y_test, y_pred)
## [1] 0.81
y_pred2 <- genie(X, 3, M=5) # clustering wrt 5-mutual reachability distance
plot(X[,1], X[,2], col=y_pred2, pch=y_test, asp=1, las=1)
noise <- is.na(y_pred2) # noise/boundary points
points(X[noise, ], col="gray", pch=10)
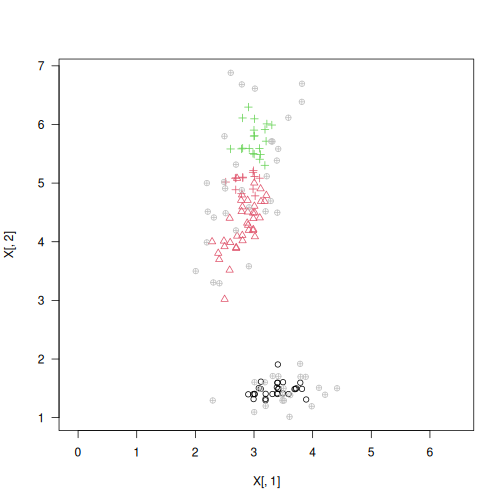
normalized_clustering_accuracy(y_test[!noise], y_pred2[!noise])
## [1] 0.8030303